Описание предпочтений
При принятии решений ЛПР исходит из собственной системы предпочтений. Цель математической теории принятия решений – разработать формальные методы, помогающие ЛПР сделать правильный выбор. Для осуществления этой цели, прежде всего, необходимо правильно отразить предпочтения ЛПР в математической модели. Как уже отмечалось, свои предпочтения ЛПР может выразить по отношению к результату своего выбора (исходу), т.е. модель его предпочтений строится на множестве исходов G. Для задач принятия решений в условиях определенности существует соответствие между множеством вариантов S и множеством исходов G ψ: S→ G. Обратное отображение ψ1: G→ S, хотя и не является в общем случае функцией (к одинаковым исходам могут вести различные стратегии), позволяет построить модель предпочтений ЛПР на множестве стратегий S. Предпочтения ЛПР можно описать различными способами. Перечислим наиболее распространенные из них.
Критерии и их шкалы
Для описания предпочтений можно использовать функции, определенные на множестве исходов G, называемые критериями. Значение критерия характеризует степень интенсивности некоторого свойства исхода, важного с точки зрения поставленной цели. Критерии могут быть числовыми (количественными) и нечисловыми (качественными). Числовой критерий – это функция K: G→ E⊆ R. Здесь E – шкала критерия, т.е. множество его допустимых значений, R – множество действительных чисел.
Шкалы критериев различают по типам. Формально нечисловые критерии всегда можно превратить в числовые, например, задав биекцию ξ: E→{1, ... , N}, отображающую шкалу нечислового критерия в балльную шкалу. Формально шкалы критериев делятся на типы в зависимости от множества допустимых для этого критерия преобразований Φ. Преобразование η критерия K называется допустимым, если функция η(K) выражает тот же признак, что и критерий K. Чем совершеннее шкала, тем уже множество Φ.
Количественные критерии могут обладать:
1. Абсолютной шкалой. Измерения, производимые в этой шкале, имеют однозначный числовой результат. Например, количество мест в аудитории или количество работников, необходимых для выполнения конкретной операции. Для абсолютной шкалы множество допустимых преобразований состоит из единственного тождественного отображения Φ = {η(x) | η(x) = x}.
2. Шкалой интервалов. Результат измерений, производимых в этой шкале, зависит от выбора начала отсчета и масштаба (единицы измерения). Этот тип шкалы называется так потому, что при переходе от одной системы измерений к другой сохраняется отношение разностей числовых оценок. Например, температуру можно измерять по шкалам Цельсия, Фаренгейта, Реомюра, Кельвина. Известно, что разница между соседними значениями на шкале Фаренгейта, привычной для американцев, соответствует 5/9 одного деления шкалы Цельсия, принятой в Европе. Частными случаями шкалы интервалов являются шкала отношений (когда меняется только масштаб, но не меняется начало отсчета – как, например, вес можно измерять в фунтах и в килограммах) и шкала разностей (когда не меняется масштаб, но меняется начало отсчета – так, например, связаны между собой температурные шкалы Кельвина и Цельсия). Для шкалы интервалов множество допустимых преобразований состоит из всех линейных функций Φ = {η(x) | η(x) = kx+b, k>0}. При k=1 получим шкалу разностей, при b=0 – шкалу отношений.
Среди шкал качественных критериев различают
1. Номинальную шкалу. Такая шкала служит для классификации вариантов. Эта классификация не имеет оттенка превосходства одного объекта над другим. Оценка по такому критерию подчеркивает, что объекты различны. Примером измерения по такой шкале является номер или наименование группы, в которой учится студент. Для номинальных шкал допустимым преобразованием является любая биекция.
2. Порядковая шкала. Такая шкала также служит для классификации вариантов, но, в отличие от предыдущего случая, классы для таких шкал упорядочены по предпочтительности. Например, продукты делят на категории «высший сорт», «первый сорт», «второй сорт», «нестандартные», а школьные оценки – на «отлично», «хорошо», «удовлетворительно», «неудовлетворительно». Для порядковых шкал допустимым преобразованием является любая монотонно возрастающая функция.
Тип шкалы критерия необходимо учитывать при выборе метода поддержки принятия решения. Так, оценки исходов по номинальным шкалам можно лишь проверить на совпадение. Для порядковых шкал уже имеет смысл проверять, у какого из исходов оценка по критерию «лучше» (например, больше), но вычислять разности между оценками двух исходов или умножать эти оценки на какие-либо «коэффициенты важности» для качественных критериев смысла не имеет. Подобные операции при выполнении определенных условий можно выполнять лишь с количественными критериями.
В некоторых случаях предпочтения ЛПР удается описать с помощью единственного критерия K. В терминах описания предпочтений этот единственный критерий называется функцией предпочтений. Если этот критерий обладает балльной шкалой, то имеет место балльное оценивание.
В большинстве случаев для описания предпочтений ЛПР потребуется n критериев K1 , … , Kn. Значение xi = Ki (g) называется оценкой исхода g по критерию Ki, а вектор x =(x1 ,…xn ), составленный из оценок исхода g по каждому из критериев Ki, называется векторной оценкой исхода g.
Если любые два различных исхода имеют различные оценки по данной шкале, то она называется строгой (в противном случае – нестрогой).
Бинарные отношения предпочтения и функция выбора
Пусть имеется некоторое множество объектов A. Как известно, бинарным отношением ρ, заданным на множестве A, называется любое подмножество множества A×A; то есть бинарное отношение – это множество упорядоченных пар
ρ = {
Если a,b∈ρ, то говорят, что a находится с b в отношении ρ и пишут aρb.
В теории принятия решений нас будет интересовать множество A, являющееся либо множеством исходов G, либо множеством стратегий S, либо множеством критериев K. Мы будем рассматривать не всякие бинарные отношения ρ, а только отношения предпочтения. Имеется четыре вида отношений предпочтения, различающихся предикатом Πp (a,b), который выражает мнение ЛПР о сравнительной предпочтительности для каждой пары объектов a и b:
• Отношением строгого предпочтения P называют бинарное отношение, для которого предикат Πp(a,b) означает «объект a предпочтительнее объекта b».
• Отношением нестрогого предпочтения R называют бинарное отношение, для которого предикат ΠR(a,b) означает «объект a не хуже объекта b».
• Отношением безразличия I называют бинарное отношение, для которого предикат ΠI(a,b) означает «объекты a и b равнопредпочтительны».
• Отношением несравнимости N называют бинарное отношение, для которого предикат ΠN(a,b) означает «объекты a и b несравнимы».
Исходя из гипотезы рациональности поведения ЛПР, легко понять, как должны быть связаны между собой отношения P, R, I и N:
R = P∪I; P = R\I; I = R∩R-1; P∩I = Ø; N = A×A\(R∪R-1).
Из приведенных соотношений видно, что по отношению R (или по паре отношений P, I) можно определить остальные отношения.
Отношение предпочтения удобно изображать в виде ориентированного графа, в котором вершины соответствуют сравниваемым объектам, а дуги – парам объектов, входящим в бинарное отношение.
Пример 2.1.
Пусть на множестве A = {a,b,c} задано отношение нестрогого предпочтения R = {a,a; b,b; c,c; a,b; c,b}. Ему соответствует граф, изображенный на рис. 2.1.

Рис. 2.1. Граф отношения предпочтения.
Напомним некоторые свойства бинарных отношений и посмотрим, какие из них характерны для отношений предпочтения.
Отношение ρ называют рефлексивным, если для всех a выполнено aρa, и антирефлексивным, если для всех a не выполнено aρa.
Очевидно, что отношения I и R являются рефлексивными, отношения P и N – антирефлексивными.
Отношение ρ называют симметричным, если для всех a, b из aρb следует bρa; антисимметричным, если из aρb, bρa следует a=b; асимметричным, если из aρb следует, что bρa – не выполнено.
Очевидно, что отношения I и N являются симметричными, отношение P – асимметричным, R – в общем случае не обладает ни одним из свойств, связанных с симметрией.
Отношение ρ называют транзитивным, если для всех a,b,c из aρb, bρc следует aρc.
В большинстве методов поддержки принятия решений отношения P, I и R считают транзитивными. Однако в общем случае эти отношения, как и отношение N, транзитивными не являются. Одна из основных причин нетранзитивности отношения предпочтения – это переход от оценки объектов по одному признаку к оценке по другому. В главе 7 приводится пример нетранзитивного отношения P, построенного по такому часто используемому правилу, как правило, большинства в задаче группового выбора.
Пример 2.2.
Пусть имеется последовательность объектов a1, a2, … , ak, такая, что объекты близки по качеству, но каждый следующий незначительно лучше предыдущего. Тогда мнение ЛПР для каждой пары соседних объектов будет ai+1Iai, но если ЛПР сравнит ak и a1, то окажется, что akPa1.
Отношение ρ называют полным, если для всех a,b выполнено aρb или bρa.
Если отношение R является полным, то имеет место ранжирование объектов множества А, то есть представление элементов множества A в виде последовательности в порядке убывания (или невозрастания) предпочтительности. Если при этом отношение I содержит только пары вида (a,a), то ранжирование будет полным.
Функцией выбора называют функцию Y = C(X), ставящую в соответствие произвольному набору альтернативных вариантов X, называемому предъявлением, его подмножество Y, называемое выбором из данного предъявления. Подробно о свойствах функций выбора рассказывается в главе 3.
По отношению нестрогого предпочтения R можно построить функцию выбора, используя одно из правил:
1. Объект a* выбирается из множества X⊆A, если a* является наилучшим во множестве X, т.е. выполняется a*Ra для любого a∈A.
C1(X) = {a* | ∀a∈X a*Ra}. Все объекты, попавшие в выбор C1(X), находятся между собой в отношении I: если a, b∈ A , то aIb.
2. Объект a* выбирается из множества X⊆A, если a* является максимальным (недоминируемым) во множестве X, т.е. не существует такого a∈A, что aPa*. C2 (X) = {a* | ∄a∈A: aP a*}.
Пример 2.3.
Для отношения из примера 2.1: C1({a,b,c}) = ∅, C2({a,b,c}) = {a,c}.
Одним из способов формирования отношения предпочтения является представление его в виде числовой функции. Говорят, что отношение нестрогого предпочтения R на А представляет числовая функция f, если aRb ⇔ f(a)Ͱf(b). Функцию f:A→R𝓡 (где R𝓡 – множество действительных чисел), обладающую указанным свойством, называют функцией полезности (или функцией ценности). Понятно, что при этом aIb ⇔ f(a)=f(b), aPb ⇔ f(a)>f(b).
Заметим, что если функция полезности существует, то отношение несравнимости N=Ø. В этом случае имеет место ранжирование объектов. Обратная задача – нахождение функции полезности по отношению предпочтения имеет решение, если R – полное отношение.
Если предпочтения ЛПР описываются n критериями и известны векторные оценки всех вариантов, то по ним можно построить отношения предпочтения различными способами. Рассмотрим основные способы. Пусть x – векторная оценка варианта a, y – векторная оценка варианта b; все критерии максимизируются.
Отношение Парето P0 определяется следующим образом: вариант a с векторной оценкой x предпочтительнее варианта b с векторной оценкой y по отношению Парето, если оценки варианта a по всем критериям не хуже оценок варианта b, и хотя бы по одному критерию лучше:
aP0b ⇔ ( xi≥ yi, ∀i=1,…,n и ∃j: xj> yj, j∈{1,…,n}).
Отношение безразличия I0 для отношения Парето является отношением равенства векторных оценок объектов: aI0 b ⇔ x=y.
Отношение нестрогого предпочтения по Парето R0 определяется соотношениями aP0 b ⇔ xi≥ yi, ∀i=1,…,n.
Отношение лексикографического порядка L определяется следующим образом: вариант a с векторной оценкой x предпочтительнее варианта b с векторной оценкой y по отношению лексикографического порядка, если он обладает лучшей, чем у b, оценкой по некоторому критерию, а для всех критериев с меньшими номерами (если таковые есть) варианты a и b имеют равные оценки.
aLb ⇔ ∃i: ∃i∈{1,…,n}, xj = yj при j=1,…,i-1, xj >yj ,.
Замечание 1. Знаки неравенств в определениях следует заменить на противоположные, если критерии минимизируются.
Замечание 2. Если Р – отношение строгого предпочтения, то P0⊆P.
Замечание 3. Отношение Парето P0 является моделью предпочтений (p) ЛПР для многокритериальных задач (см. постановку ЗПР) в случае, если дополнительная информация (ς) о предпочтениях отсутствует.
Отношение лексикографического порядка L является моделью предпочтений (p) ЛПР для многокритериальных задач в случае, если дополнительная информация (ς) имеет вид «критерий K1 важнее всех остальных, критерий K2 в свою очередь важнее всех, кроме K1 и т.д.».
Пример 2.4. Рассмотрим задачу с четырьмя вариантами x, y, z, u, которые оцениваются по трем максимизируемым критериям K1, K2, K3. Векторные оценки вариантов по критериям представлены в таблице 2.1. Графы отношений Парето P0 и лексикографического порядка L изображены на рис. 2.2 и 2.3.

Рис 2.2. Граф отношения P0 Рис 2.3. Граф отношения L
Элементы теории выбора
Выбор наилучшего решения на основе попарного сравнения всех возможных решений, т.е. выбор на основе формирования бинарного отношения предпочтения (иными словами, парнодоминантного принципа сравнения) эмоционально кажется вполне разумным. Но некоторые простые примеры показывают, что это не всегда так. Например, в спортивных соревнованиях для определения победителя используют турнирную таблицу (3 очка начисляется за победу, 1 очко за ничью, 0 очков за поражение). При этом из того, что команда «X» победила команду «Y» в личной встрече (т.е. команда «X» сильнее команды «Y») не следует, что команда «X» окажется выше команды «Y» по результатам всего турнира. В этом примере выбор осуществляется не на основе построения бинарного отношения, а на основе иного механизма. Изучением закономерностей процесса выбора занимается теория выбора [1].
Общая модель выбора представлена на рис.3.1:
Рис.3.1. Модель выбора
В результате преобразования выбора каждому X ставится в соответствие Y⊆ X и возникает функция выбора Y = C(X).
Характеристические свойства функций выбора
Рассмотрим ряд условий, которые выражают различные естественные требования к разумному выбору.
Будем говорить, что функция выбора C(X) удовлетворяет условию наследования (Н), если ∀ X, X’ ∈ A выполняется условие:
[ X’⊆X ] ⇒ [ C(X)∩X’⊆C(X’) ].
То есть если сузить предъявление, отбросив часть вариантов, то все варианты из суженного множества X’, которые были выбраны из исходного множества X, также попадут в выбор из X’. Например, товары, выбранные из широкого ассортимента, естественно, будут выбраны и из содержащего их более узкого ассортимента.
Заметим, что это условие не исключает того, что в выбор из X’ попадут еще какие-то варианты, которые в выбор из X не попали.
<Усилим условие Н. Будем говорить, что функция выбора C(X) удовлетворяет условию строгого наследования или константности (К) выбора, если ∀X, X’ ∈ A выполняется условие:
[ X’⊆ X ] ⇒ [ если C(X)=∅, то C(X’)=∅, а если C(X)∩X’≠∅, то C(X’)=C(X)∩X’ ].
То есть все выбранные из X варианты, и только они, попадают в выбор из X’, если, конечно, они в X’ содержатся. Если выбор из X был пуст, то и выбор из X’ будет пуст. И только если пересечение множеств C(X) и X’ пусто, а множество C(X) не является пустым, то C(X’) может содержать какие-то другие варианты.
Пример 3.1. Вы выбрали какие-то товары в каталоге (X – множество товаров в каталоге, C(X) – ваш выбор из этого предъявления) и пришли в магазин. Если в наличии (X’ – ассортимент магазина) имеются какие-то из выбранных вами по каталогу товаров (C(X)∩X’ ), то именно их вы и выберете (C(X’) – ваш выбор из ассортимента магазина). Если же ни одного из выбранных вами по каталогу товаров в наличии нет, то вы, возможно, выберете что-то другое. А если вам изначально ничего не понравилось в каталоге, то вы и не пойдете в этот магазин.
Функция выбора C(X) удовлетворяет условию согласия (С), если ∀ X’, X’’ ∈ A выполняется условие:
[ X = X’∪X’’ ] ⇒ [ C(X’)∩ C(X’’)⊆C(X) ].
То есть все варианты, выбираемые и из X’ и X’’ по отдельности, должны выбираться и из объединения X’∪X’’. Хотя в этот выбор могут попасть и другие варианты.
Пример 3.2. В одном доме находятся два магазина. X’ – ассортимент первого магазина, X’’ – ассортимент второго магазина. Вы заходите в любой из этих магазинов, чтобы купить чай и чего-нибудь к чаю. В обоих магазинах есть чай “Со слоном”, который вам больше всего нравится. А вот сладости в ассортиментах этих магазинов представлены по-разному. Из того, что продается в первом магазине, вам больше всего нравятся вафли “Прохладительные”. А если вы идете во второй магазин, то покупаете там конфеты “Теннис”. Таким образом, C(X’)={“Со слоном”, “Прохладительные”}, C(X’’)={“Со слоном”, “Теннис”}. Теперь представим, что эти магазины объединятся в один магазин с общим ассортиментом X = X’∪X’’. В таком случае, в ваш выбор C(X), естественно, по-прежнему войдет чай {“Со слоном”} = C(X’)∩C(X’’). А вот что вы будете покупать к чаю, неизвестно.
Функция выбора C(X) удовлетворяет условию независимости от отбрасывания отвергнутых вариантов (О), если ∀X, X’ ∈ A выполняется условие:
[ C(X)⊆X’⊆X ] ⇒ [ C(X’) = C(X) ].
То есть сужение предъявления за счет отбрасывания некоторых или всех невыбранных вариантов не изменяет выбор.
Пример 3.3. На ваш выбор в магазине (C(X’)) никак не повлияет отсутствие товаров, которые не понравились вам в каталоге (C(X)⊆X’⊆X ).
Будем обозначать символами Н, С, О и К множества функций выбора, удовлетворяющих соответствующим условиям.
Пример 3.4. Примеры функций выбора.
В таблице 3.1 приведены восемь различных функций выбора из трехэлементного множества A={x,y,z}. Строки, соответствующие одноэлементным предъявлениям, в эту таблицу не включены. Подразумевается, что в таких ситуациях выбор совпадает с предъявлением (C({x})={x}, C({y})={y}, C({z})={z}). В последней строке указано, какими из свойств обладают эти функции. Из этого примера видно, что существуют функции с любым сочетанием свойств Н, С, О.
Таблица 3.1

Пример 3.5. Пример функции выбора, не удовлетворяющей условию K.
Следующий пример показывает, что существуют функции выбора, удовлетворяющие условиям Н, С, О, но не удовлетворяющие условию K.
Пусть A = {x} ∪ V, V = {v1, …, vt}; C(X) = {{x,vj} | j=min{k | vk∈X}}, если x∈X, C(X) = {{vj} | j=min {k | vk∈X}}, если x∉X.
Тогда С({x,v1,v2}) = {x,v1}, С({x,v2}) = {x,v2}, следовательно, условие константности выбора не выполнено. Легко проверить, что условия наследования, согласования и отбрасывания для такой функции выполняются.
Из определений непосредственно следует, что условие К влечет выполнение условия Н, условие К влечет выполнение условия О. Покажем, что справедливо также то, что из условия К следует свойство С. Пусть y∈C(X’)∩C(X’’). Предположим, что y∉C(X’∪X’’). Тогда, если C(X’∪X’’)=Ø, то по условию К C(X’)=C(X’’)=Ø, что противоречит условию y∈C(X’)∩C(X’’). Если x∈X’, то по условию К C(X’) = C(X’∪X’’)∩X’, следовательно y∉C(X’). Аналогично рассматривается случай x∈X’’. Из проведенных рассуждений и приведенных примеров следует справедливость следующего утверждения.
Теорема 3.1. Условия Н, С, О независимы (т.е. все возможные пересечения множеств Н, С, О и их дополнений не пусты), условие К является усилением каждого из условий Н, С, О (т.е. К⊂Н∩С∩О).
Взаимосвязь между свойствами функций выбора и свойствами отношения предпочтения
Рассмотрим один из наиболее распространенных способов задания функции выбора, который уже упоминался в главе 2. Пусть известно отношение P строгого предпочтения ЛПР на множестве объектов A. Тогда функция выбора может быть задана следующим образом: для любого предъявления X⊆A выбор С:
C(X) = { a* | ∄a∈ X: aP a*}. Возникает вопрос о том, как связаны между собой свойства отношения предпочтения P и свойства функции выбора, построенной на его основе. Ответ на этот вопрос представлен в таблице 3.1.
Таблица 3.1
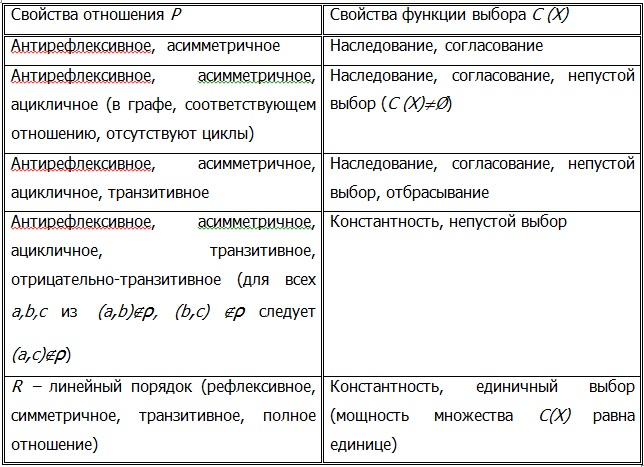
Заметим, что свойства, представленные в строках этой таблицы, расположены в порядке нарастания требований.
Условия Кондорсе для функций выбора
Если справедливо условие Н, то справедливо и следующее более слабое условие: ∀X ∈ A верно, что [ x∈C(X) ] ⇒ [ x∈C({ x, y }) ∀ y∈X ]. Это условие называется обратным условием Кондорсе (Cor- ). Оно означает, что если вариант выбирается из X, то он выбирается и из любой содержащей его пары вариантов.
Если справедливо условие
С, то справедливо и следующее, более слабое условие: ∀X ∈ A верно, что [ ∀y∈X x∈C({ x, y }) ] ∈ [ x∈C(X) ]. Это условие называется прямым условием Кондорсе (Con+). Оно означает, что если вариант выбирается из всех содержащих его парных предъявлений, то он выбирается из X.
Функция выбора удовлетворяет принципу Кондорсе, если для неё одновременно выполняются условия Con- и Con+.
Теорема 3.2. Множества Con- ∩ Con+ и Н∩С совпадают.