Элементы теории выбора
Выбор наилучшего решения на основе попарного сравнения всех возможных решений, т.е. выбор на основе формирования бинарного отношения предпочтения (иными словами, парнодоминантного принципа сравнения) эмоционально кажется вполне разумным. Но некоторые простые примеры показывают, что это не всегда так. Например, в спортивных соревнованиях для определения победителя используют турнирную таблицу (3 очка начисляется за победу, 1 очко за ничью, 0 очков за поражение). При этом из того, что команда «X» победила команду «Y» в личной встрече (т.е. команда «X» сильнее команды «Y») не следует, что команда «X» окажется выше команды «Y» по результатам всего турнира. В этом примере выбор осуществляется не на основе построения бинарного отношения, а на основе иного механизма. Изучением закономерностей процесса выбора занимается теория выбора [1].
Пусть задано множество вариантов A. В содержательных задачах роль вариантов могут играть кандидаты, планы, стратегии, проекты, товары и т.п. Будем считать, что A – конечное множество из двух или более элементов. Пусть далее A – некоторое заданное множество непустых подмножеств X вариантов из A. Любое подмножество X∈A может быть предъявлено для осуществления акта выбора и называется далее предъявлением. В специально оговариваемых случаях могут вводиться ограничения на A (например, A содержит пары вариантов из A и т.п.). Акт выбора состоит в выделении из предъявления X∈A по некоторому фиксированному правилу подмножества Y⊆X, называемого «выбор из X» или в установлении факта отказа от выбора. В последнем случае говорят, что выбор пуст (Y=∅).
Общая модель выбора представлена на рис.3.1:

В результате преобразования выбора каждому X ставится в соответствие Y⊆X и возникает функция выбора Y = C(X).
Характеристические свойства функций выбора
Рассмотрим ряд условий, которые выражают различные естественные требования к разумному выбору.
Будем говорить, что функция выбора C(X) удовлетворяет условию наследования (Н), если ∀ X, X' ∈ A выполняется условие:
[ X'⊆ X ] ⇒ [ C(X)∩X'⊆ C(X') ].
То есть если сузить предъявление, отбросив часть вариантов, то все варианты из суженного множества X', которые были выбраны из исходного множества X, также попадут в выбор из X'. Например, товары, выбранные из широкого ассортимента, естественно, будут выбраны и из содержащего их более узкого ассортимента.
Заметим, что это условие не исключает того, что в выбор из X' попадут еще какие-то варианты, которые в выбор из X не попали.
Усилим условие Н. Будем говорить, что функция выбора C(X) удовлетворяет условию строгого наследования или константности (К) выбора, если ∀ X, X' ∈ A выполняется условие:
[ X'⊆ X ] ⇒ [ если C(X)=∅, то C(X')=∅,
а если C(X)∩X'≠ ∅, то C(X')=C(X)∩X' ].
То есть все выбранные из X варианты, и только они, попадают в выбор из X', если, конечно, они в X' содержатся. Если выбор из X был пуст, то и выбор из X' будет пуст. И только если пересечение множеств C(X) и X' пусто, а множество C(X) не является пустым, то C(X') может содержать какие-то другие варианты.
Пример 3.1. Вы выбрали какие-то товары в каталоге (X – множество товаров в каталоге, C(X) – ваш выбор из этого предъявления) и пришли в магазин. Если в наличии (X' – ассортимент магазина) имеются какие-то из выбранных вами по каталогу товаров (C(X)∩X' ), то именно их вы и выберете (C(X') – ваш выбор из ассортимента магазина). Если же ни одного из выбранных вами по каталогу товаров в наличии нет, то вы, возможно, выберете что-то другое. А если вам изначально ничего не понравилось в каталоге, то вы и не пойдете в этот магазин.
Функция выбора C(X) удовлетворяет условию согласия (С), если ∀X', X'' ∈ A выполняется условие:
[ X = X'∪ X'' ] ⇒ [ C(X')∩C(X'')⊆C(X) ].
То есть все варианты, выбираемые и из X' и X'' по отдельности, должны выбираться и из объединения X'∪X''. Хотя в этот выбор могут попасть и другие варианты.
Пример 3.2. В одном доме находятся два магазина. X' – ассортимент первого магазина, X'' – ассортимент второго магазина. Вы заходите в любой из этих магазинов, чтобы купить чай и чего-нибудь к чаю. В обоих магазинах есть чай “Со слоном”, который вам больше всего нравится. А вот сладости в ассортиментах этих магазинов представлены по-разному. Из того, что продается в первом магазине, вам больше всего нравятся вафли “Прохладительные”. А если вы идете во второй магазин, то покупаете там конфеты “Теннис”. Таким образом, C(X')={“Со слоном”, “Прохладительные”}, C(X'')={“Со слоном”, “Теннис”}. Теперь представим, что эти магазины объединятся в один магазин с общим ассортиментом X = X'∪ X''. В таком случае, в ваш выбор C(X), естественно, по-прежнему войдет чай {“Со слоном”} = C(X')∩C(X''). А вот что вы будете покупать к чаю, неизвестно.
Функция выбора C(X) удовлетворяет условию независимости от отбрасывания отвергнутых вариантов (О), если ∀X, X' ∈ A выполняется условие:
[ C(X)⊆X'⊆X ] ⇒ [ C(X') = C(X) ].
То есть сужение предъявления за счет отбрасывания некоторых или всех невыбранных вариантов не изменяет выбор.
Пример 3.3. На ваш выбор в магазине (C(X')) никак не повлияет отсутствие товаров, которые не понравились вам в каталоге (C(X)⊆X'⊆X ).
Будем обозначать символами Н, С, О и К множества функций выбора, удовлетворяющих соответствующим условиям.
Пример 3.4. Примеры функций выбора.
В таблице 3.1 приведены восемь различных функций выбора из трехэлементного множества A={x,y,z}. Строки, соответствующие одноэлементным предъявлениям, в эту таблицу не включены. Подразумевается, что в таких ситуациях выбор совпадает с предъявлением (C({x})={x}, C({y})={y}, C({z})={z}). В последней строке указано, какими из свойств обладают эти функции. Из этого примера видно, что существуют функции с любым сочетанием свойств Н, С, О.

Пример 3.5. Пример функции выбора, не удовлетворяющей условию K.
Следующий пример показывает, что существуют функции выбора, удовлетворяющие условиям Н, С, О, но не удовлетворяющие условию K.
Пусть A = {x} ∪ V, V = {v1, …, vt}; C(X) = {{x,vj} | j=min{k | vk∈X}}, если x∈X, C(X) = {{vj} | j=min {k | vk∈X}}, если x∉X.
Тогда С({x,v1,v2}) = {x,v1}, С({x,v2}) = {x,v2}, следовательно, условие константности выбора не выполнено. Легко проверить, что условия наследования, согласования и отбрасывания для такой функции выполняются.
Из определений непосредственно следует, что условие К влечет выполнение условия Н, условие К влечет выполнение условия О. Покажем, что справедливо также то, что из условия К следует свойство С. Пусть y∈C(X')∩C(X''). Предположим, что y∉C(X'∪X''). Тогда, если C(X'∪X'')=Ø, то по условию К C(X')=C(X'')=Ø, что противоречит условию y∈C(X')∩C(X''). Если x∈X', то по условию К C(X') = C(X'∪X'')∩X', следовательно y∉C(X'). Аналогично рассматривается случай x∈X''. Из проведенных рассуждений и приведенных примеров следует справедливость следующего утверждения.
Теорема 3.1. Условия Н, С, О независимы (т.е. все возможные пересечения множеств Н, С, О и их дополнений не пусты), условие К является усилением каждого из условий Н, С, О (т.е. К⊂Н∩С∩О).
Взаимосвязь между свойствами функций выбора и свойствами отношения предпочтения
Рассмотрим один из наиболее распространенных способов задания функции выбора, который уже упоминался в главе 2. Пусть известно отношение P строгого предпочтения ЛПР на множестве объектов A. Тогда функция выбора может быть задана следующим образом: для любого предъявления X⊆A выбор С: C(X) = { a* | ∄a∈X: aPa*}. Возникает вопрос о том, как связаны между собой свойства отношения предпочтения P и свойства функции выбора, построенной на его основе. Ответ на этот вопрос представлен в таблице 3.1.
Таблица 3.1
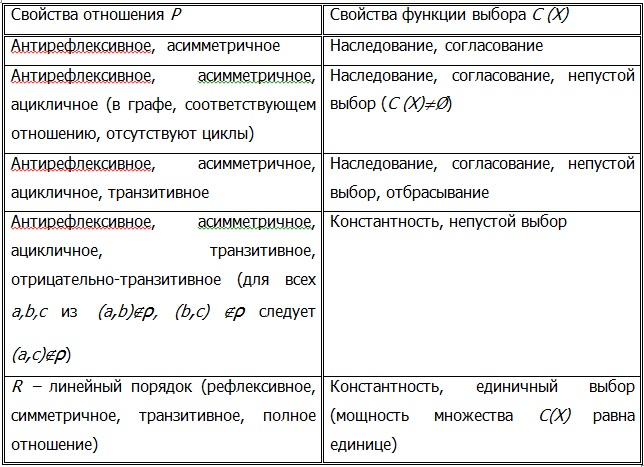
Заметим, что свойства, представленные в строках этой таблицы, расположены в порядке нарастания требований.
Условия Кондорсе для функций выбора
Если справедливо условие Н, то справедливо и следующее более слабое условие: ∀ X ∈ A верно, что [ x∈C(X) ] ⇒ [ x∈C({ x, y }) ∀ y∈X ]. Это условие называется обратным условием Кондорсе (Con-). Оно означает, что если вариант выбирается из X, то он выбирается и из любой содержащей его пары вариантов.
Если справедливо условие С, то справедливо и следующее, более слабое условие: ∀ X ∈ A верно, что [ ∀ y∈X x∈C({ x, y }) ] ⇒ [ x∈C(X) ]. Это условие называется прямым условием Кондорсе (Con+). Оно означает, что если вариант выбирается из всех содержащих его парных предъявлений, то он выбирается из X.
Функция выбора удовлетворяет принципу Кондорсе, если для неё одновременно выполняются условия Con- и Con+.
Теорема 3.2. Множества Con-∩Con+ и Н∩С совпадают.